Hindutva, Mathematics, Pythagoras and Zero
The Hindutva brigade have been continuously proclaiming that the Greeks learnt Pythagoras from India. This is what Harsh Vardhan, the BJP Science and Technology Minister, claimed in the Indian Science Congress last year; that “we” discovered the Pythagoras theorem and gave it “magnanimously” to the Greeks. There have also been claims of Vedic mathematics, which is sought to be introduced in the schools as advanced mathematics of the Vedas. In this vain glorious view of history, what we miss are the real advances that India made in mathematics.
The Pythagoras Theorem
The Pythagoras theorem, in its most well-known version states that in a right angled triangle, the square on the hypotenuse (the side opposite the right angle) is equal to the square on the other two sides. A set of numbers that satisfies this relationship is called Pythagorean tuples.
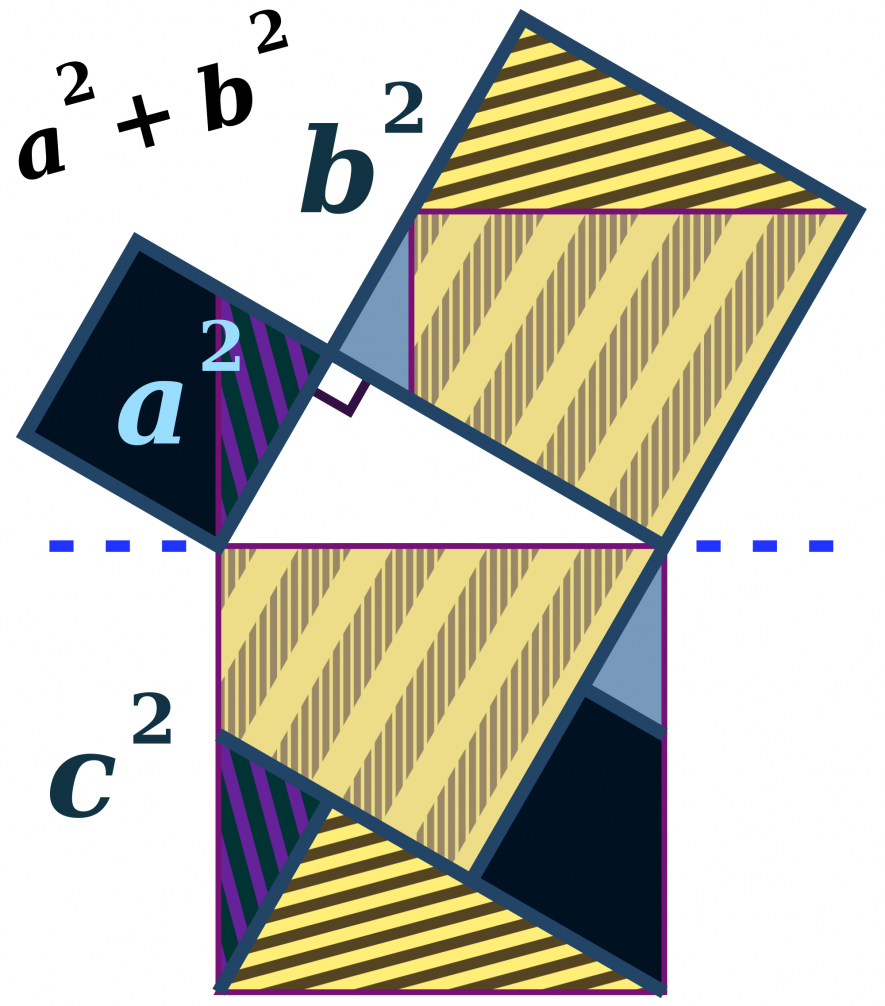
Image Courtesy: commons.wikimedia.org
The basis of the claims regarding the Pythagoras thorem, is the Sulba-sutras, the texts that tell us how to make different kinds of altars or vedis for religious purposes. There are four important Sulba-sutras, that of Baudhayana (c 800 BCE), Apastamba (c 600 BCE), Manava (c 750 BCE) and Katyayana (c 200 BCE). The Sulba-sutras are a part of Vedanga Jyotisha, and are therefore a part of Bramhanical rituals.
The Sulba-sutras gives us formulations of the theorem, using rectangles instead of triangles, as we write it today. It is clear from the texts of the Sulba-sutras, that the authors knew the geometrical relationships between the three sides of a right-angled triangle and also knew a set of numbers that satisfy this relationship. This allowed the construction of complicated fire altars by being able to create right angled triangles.
The Pythagoras theorem was known in India, Babylon, China and in Egypt and used for land measurement, the construction of religious structures (pyramids in Egypt and the fire altars) and for constructing canals (Babylon). There are Babylonian tablets used for teaching scribes that predate the Sulba-sutras – they date to 1800 BCE -- and show a knowledge of Pythagorean tuples and the Pythagoras theorem. It is also known that Babylon and Egypt routinely exchanged goods, knowledge and texts. Egypt, either independently, or from Babylon, also knew about Pythagoras theorem. It is also known that Pythagoras spent a considerable part of his early life in Egypt and learned his mathematics from the Egyptians. The Chinese also knew about the Pythagoras theorem; in China it was known as the kou-ku theorem.
The claim to fame is of Pythagoras that he was supposedly the first to provide a formal proof of the theorem. Baudhayan provides a proof for isosceles, right-angled triangles, while Apastamba gives a numerical proof of the more general statement, true for any right angled triangle. The Chinese had also developed a proof of the Pythagoras theorem, but in a visual form.
Neither is the Eurocentric claim that Pythagoras provided the first proof valid, nor the Indocentric view that India was the original home of the Pythagoras theorem.
The Pythagoras theorem shows how the history of science and mathematics is not one of who did what first, but to see the broad sweep of development and what have been the contributions of each cultural area. It is very different from cultural supremacist claims of any specific culture.
Zero and the Indian Number System
The history of India's development of the modern number system and the zero is similar. Apart from the actual symbols of the numbers, there are three important elements that constitute the modern number system – the place value notation, the base 10 and the use of zero as a number.
Babylon and India made major contributions in the development of the place value notation. In this notation, a number has a value based on the position it occupies in the number; eg., in 66, though both the numbers are six, the value of the first 6 is sixty, the second 6 is six. In Roman numerals, it would be written as LXVI, where L is fifty, X is ten, V is five and I is 1.
In the Roman number system, computations are obviously extremely cumbersome. The place value notation makes the basic arithmetic operations, addition, subtraction, multiplication and division, much simpler allowing for the complex calculations required in commerce, engineering, astronomy and physics. Ptolemy, in his astronomical text Almagest, uses the Babylonian system for his calculations, though expresses them finally in the Roman numerals.
Though the Babylonians had developed the place value notation earlier, they used a sexagesimal system or base 60, while India used the base 10 system, which we all now use. The Babylonian sexagesimal system still persists in our calculations for time: an hour is divided into 60 minutes, and one minute into 60 seconds.
Aryabhata marks the beginning of classical age of Indian mathematics. He was born in 476 AD, had clearly formulated the place value notation in his magnum opus, Aryabatiya. He enunciated the rule "Sthanam sthanam dasa gunam," meaning from place to place, multiply by 10. The Bhakshali manuscript, found near Peshawar, has been dated to 2nd to 4th century AD for its knowledge, though the actual manuscript is held to be a copy of older texts. It shows use of the place value notation.
The use of a symbol as a marker for absence of a number, is again available in Babylon. Babylonians used various symbols to indicate the lack of a number in that position in the place value system. Ptolemy also used a null symbol in his calculations.
The major contribution of Indian mathematicians was to treat zero not as a null symbol, but as a number, and provide the rules for its use in arithmetical operations. Varahamihira, a younger contemporary of Aryabhata, was the first to use zero in mathematical operations. However, Bramhagupta was the first to formulate the mathematical rules for using zero as a number. While he correctly formulated rules for addition, subtraction and multiplication by zero, he ran into problems with division by zero. Modern mathematics has “solved” this problem by banning the operation itself!
It is also interesting to note that the Indian number system not only evolved the three major components of the system -- the place value notation, base 10 and the use of zero as a number -- it also provided the current symbols of the numbers themselves. These are derived from numerals used in the Bramhi script. Brahmi was widely used to write Prakrit, in which the major Jain mathematical texts were composed. Unlike the Vedas or the Vedanga Jyotisha, Jain mathematical texts were not based on Bramhanical rituals. Jains believed that mathematics itself was an exercise in reaching higher consciousness, much like the Pythagoreans in Greece.
Vedic Mathematics Versus real Mathematics
As always happens with the Hindutva brigade, they are not satisfied by claiming the real advances that took place in Indian mathematics. They also must make fraudulent claims for the wisdom of the Vedas and its advanced knowledge. Such claims have been made by Swami Bharati Krishna Tirthaji, the late Shankaracharya of Puri, regarding what he called “Vedic” mathematics. Professor SG Dani and others have shown that this has nothing to do with ancient mathematics or the Vedas. Though claiming for itself the antiquity of Atharvaveda, no such text of Atharvadeda has been found in the existing literature on the Vedas.
This so-called Vedic mathematics is just a set of tricks or gimmicks for some specific calculations. It has little to do with mathematics as we know it today, and in the age of calculators and computers, has virtually no value.
The other problem with the Hindutva brigade's focussing on the Vedas and the epics – Ramayana and Mahabharata – as the sole source of wisdom, is that it then misses out all other advances that Indian mathematics did in the later period. Aryabhata had derived the value of pi to 5 decimal places, the most accurate derivation for his times. Indian mathematicians such as Aryabhata, Bramhagupta, Bhaskara I (5th-7th century), and later Bhaskara II (12th century) made significant contributions to trigonometric functions and construction of trigonometric tables. The work of Indian mathematicians, such as Madhava, Nilkantha and others, from what is now termed as the Kerala school in the 14th-16th century, gave us the series expansion of trigonometric and other functions that predate the work done in Europe.
The form of mathematics as we know today -- from axioms, hypothesis to proof – was first given in Euclid's Geometry. This was very much a part of the Greek development of mathematics. The Greeks also introduced proof using reductio absurdum: an assumption that leads to a logical contradiction, must be a wrong assumption. This is a powerful tool in the armoury of mathematics. Other civilisations, such as Babylon and India, used far superior computation systems to that of the Greeks, but did not develop this formal method of proof.
It is very much a Eurocentric view that condemns all other civilisations that did not develop the formal methods of the Greeks as “algorithmic”, only confined to “practical” mathematics and therefore inferior. What such a view forgets is that trade, commerce, developments in science and technology, rest on this “practical” ability to compute with numbers.
This modern number system was developed in Babylon and India, and then transmitted to the Arabs. Al Khwarzmi wrote a treatise on the Indian system of numerals -- Kitāb al-Ǧamʿwa-al-tafrīq bi-ḥisāb al-Hind, translated in Latin as Algoritmi de numero Indorum (al-Khwārizmī on the Hindu Art of Reckoning). The world algorithm is derived from the title of this text. Leonardo of Pisa, more commonly known as Fibonacci, popularised the Indian system of numbers in Europe through his book, Liber Abaci (Book of Calculations). Without such developments, we would not have the industrial revolution, and the birth of modern science in Europe.
There was also an exchange between all these cultures, particularly between India, Greece, Babylon and Egypt. There is the story of the great polymath Ibn Sina (known as Avicenna in the west), that his father told him not to waste his time but go and learn some mathematics from the Hindu merchant in the market.
Different cultures developed knowledge about geometry and calculations with numbers with different degrees of sophistication. If the formal nature of Greek mathematics has been a powerful instrument in the development of modern mathematics, the growth of computational methods and algorithms are the bedrock of modern science and technology.
The Hindutva lobby attempts to invert the arguments of the Eurocentric or Orientalist view of history of mathematics, with mostly empty assertions and fraudulent history. The real answer to Eurocentric “history”, is not substitute it with fraudulent history, but the real history of knowledge. And such a history does not support a supremacist version, either of a Eurocentric or Hindutva one.
Disclaimer: The views expressed here are the author's personal views, and do not necessarily represent the views of Newsclick
Get the latest reports & analysis with people's perspective on Protests, movements & deep analytical videos, discussions of the current affairs in your Telegram app. Subscribe to NewsClick's Telegram channel & get Real-Time updates on stories, as they get published on our website.
























